
Design DFA accepting Binary numbers divisible by number 'n': Note: Sometime we define partial DFA as δ ⊆ Q × Σ→Q (Read: How does “δ:Q × Σ→Q” read in the definition of a DFA). from each state in Q there is one outgoing edge present for every language symbol in Σ). In other words we can say in transition diagram of complete DFA there is no missing edge (e.g. Repeated function composition forms a monoid.Below, I have written an answer for n equals to 5, but you can apply same approach to draw DFAs for any value of n and 'any positional number system' e.g binary, ternary.įirst lean the term 'Complete DFA', A DFA defined on complete domain in δ:Q × Σ→Q is called 'Complete DFA'.
DEFINE DETERMINISTIC FINITE AUTOMATON SOFTWARE
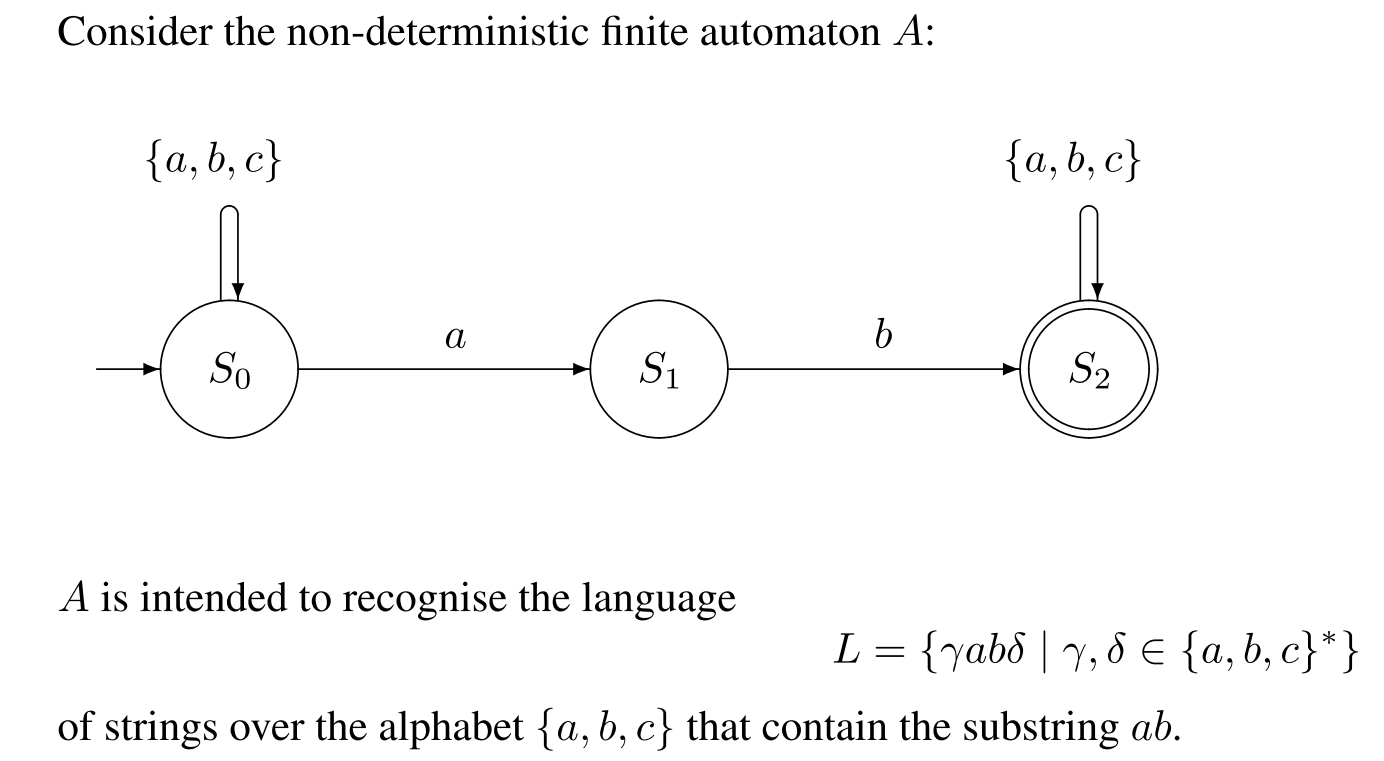
For example, a DFA can model software that decides whether or not online user input such as email addresses are syntactically valid. A DFA has a start state (denoted graphically by an arrow coming in from nowhere) where computations begin, and a set of accept states (denoted graphically by a double circle) which help define when a computation is successful.Ī DFA is defined as an abstract mathematical concept, but is often implemented in hardware and software for solving various specific problems such as lexical analysis and pattern matching. For example, if the automaton is currently in state S 0 and the current input symbol is 1, then it deterministically jumps to state S 1.
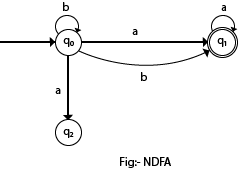
Upon reading a symbol, a DFA jumps deterministically from one state to another by following the transition arrow. For each state, there is a transition arrow leading out to a next state for both 0 and 1. The automaton takes a finite sequence of 0s and 1s as input. In this example automaton, there are three states: S 0, S 1, and S 2 (denoted graphically by circles).
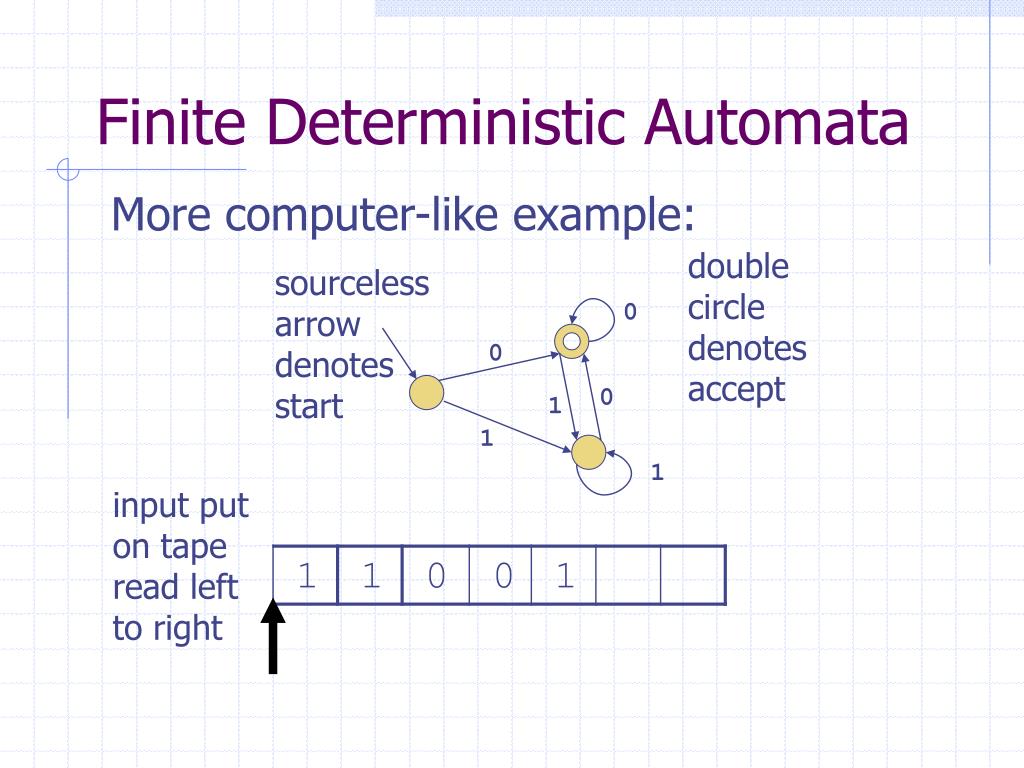
The figure illustrates a deterministic finite automaton using a state diagram. In search of the simplest models to capture finite-state machines, Warren McCulloch and Walter Pitts were among the first researchers to introduce a concept similar to finite automata in 1943.

Deterministic refers to the uniqueness of the computation run. In the theory of computation, a branch of theoretical computer science, a deterministic finite automaton ( DFA)-also known as deterministic finite acceptor ( DFA), deterministic finite-state machine ( DFSM), or deterministic finite-state automaton ( DFSA)-is a finite-state machine that accepts or rejects a given string of symbols, by running through a state sequence uniquely determined by the string. For example, the string "1001" leads to the state sequence S 0, S 1, S 2, S 1, S 0, and is hence accepted. The state S 0 is both the start state and an accept state. An example of a deterministic finite automaton that accepts only binary numbers that are multiples of 3. The term may also refer to drug-facilitated sexual assault.


 0 kommentar(er)
0 kommentar(er)
